 Minimum and maximum magnifications as a function of aperture.
Minimum and maximum magnifications as a function of aperture.
Orwell Astronomical Society (Ipswich)
Choosing an Eyepiece
Choosing an eyepiece for your telescope can be a complicated process with a range of features and requirements to be finely balanced. A good quality eyepiece can be expensive, so the decision should not be made lightly.
Magnification is often taken as the main consideration in the choice of an eyepiece but of course it is only one of several parameters and, depending on the observations to be undertaken, may not be the most important. The main characteristics of an eyepiece that should be considered are:
Unfortunately, the above characteristics are not independent and cannot be specified in isolation from one another. For example, magnification determines the size of the image but also has a major effect on the field of view and eye relief. The field of view also depends upon the details of the lens design and the number of optical elements used; these factors in turn affect the performance in terms of ghosting, scatter and aberrations.
The magnification of a telescope can be defined in several ways giving different insights into its dependence on the parameters listed above:
M = F/f = D/d = Af/Rf,
where
M = magnification
F = focal length of the Object Glass (OG)
f = focal length of the eyepiece
D = diameter of the OG
d = diameter of the exit pupil
Af = apparent field of the eyepiece
Rf = real field of the eyepiece
The eyepiece produces an image of the OG or primary mirror which is called the exit pupil or Ramsden disk. The exit pupil is seen as a bright disk when the telescope is pointed towards an extended light source. It defines the pencil of rays that emerge from the eyepiece when the telescope is pointed at a star and focussed at infinity. The diameter of the exit pupil is given by D/M or, equivalently, by f/F*D.
A large objective gathers more light and therefore gives a brighter image. A lower magnification also gives a brighter image of extended objects such as nebulae and planets because the light is concentrated into a smaller image. Both a larger objective and a smaller magnification increase the size of Ramsden disk: in this way a bright image and a large Ramsden disk are linked. However, there is a limit to the way in which these approaches can brighten an image, since if the Ramsden disk exceeds about 8 mm in diameter, the typical maximum diameter of a fully dark-adapted eye, some light will not enter the pupil and will be lost. For example, a pair of 7x50 binoculars has a Ramsden disk of 7.1 mm diameter.
Images of stars behave differently. A star is essentially a point source of light so no amount of magnification will produce an extended image. (On the assumption of perfect optics and seeing!) Therefore, the brightness of an image of a star depends on the diameter of the object glass or mirror, but not on the magnification. Thus, a high magnification eyepiece will not dim stars but can dim extended objects such as light pollution, and can be useful in increasing the contrast between stars and the background sky.
A large exit pupil requires a high quality eyepiece with accurate optical shape over a wide cross-section. Sufferers of astigmatism may find an eyepiece with a small exit pupil (say <2 mm) beneficial, and with such an eyepiece they may be able to observe without spectacles. However, a small exit pupil also means that small particles, floaters, tear-drops, etc in the eye are more visible against the light emerging from the eyepiece. For any particular observer's eye, there is an optimum exit pencil for which the eye will achieve highest acuity: typically this is around 2 mm.
Eye relief is the distance at which the observer's eye may be placed from the eyepiece to see the full field of view: this is when the exit pupil matches the pupil of the eye. In practice, there is a certain tolerance to the position of the eye within which the eye's pupil will still catch all the light emerging from the eyepiece. The eye relief can never be greater than the focal length of the eyepiece. This can become a problem, particularly for spectacle wearers, when using high magnification eyepieces with short focal length objectives, since it is the observer's pupil and not his/her spectacles that needs to be placed at the distance specified by the eye relief from the eyepiece. A Barlow lens can be used to increase the effective focal length of the objective and thereby provide a high magnification while maintaining acceptable eye relief.
The apparent field of the eyepiece is the angular diameter of the field observed when the eye is placed at the position of the exit pupil. The real field is the actual field of view in the sky observed to lie within the field stop when using the eyepiece in a telescope.
The area of the sky seen through the eyepiece is related to the magnification by Rf = Af / M. The apparent field of an eyepiece is determined by its focal length and the diameter of the lens or stop (which can limit the effective diameter) and usually lies between 40° and 70°. The diameter of the lens directly determines how much sky can be seen through the eyepiece for an objective of given focal length.
Two stars lying at angle a apart are separated by an amount:
b = F * tan(a) = F * a (for small a)
in the focal plane of the OG of the telescope (this assumes that one of the stars lies on the optical axis of the OG). To see these stars within the field of view, the field lens of the eyepiece must have a radius at least as large as b. Note that the separation b is dependent only on the focal length of the OG, and for a given size field lens of the eyepiece (diameter d), the real field increases as the focal length of the OG decreases. (This, rather than the "photographic speed" is the real reason for short focal length, rich field telescopes.)
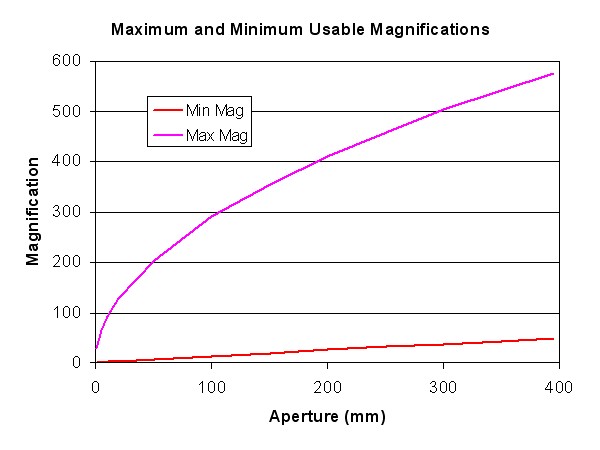
There are bounds on the range of magnification that can be usefully employed with any particular telescope. The minimum useful magnification of the telescope is determined by the constraint that the diameter of the exit pupil is at most equal to the diameter of the pupil of the observer's eye. The diameter of the eye's pupil usual lies between two and eight millimetres depending on light levels and characteristics of the individual. Typically, a fully dark adapted pupil has a diameter of circa 8 mm; this therefore defines the maximum useful diameter of the exit pupil of an eyepiece. Using the formula M=D/d it therefore follows that the minimum useful magnification, M', is given by M' = D/8 (D expressed in mm).
There is a corresponding upper limit on useful magnification determined by a combination of the resolving power of the objective and the following difficulties associated with short focal length eyepieces: increase in aberrations, reduction in eye relief, reduction in exit pupil diameter and reduction in image brightness for extended objects. An empirical expression for the maximum usable magnification, M", taking account of these factors is M" = 29*sqrt(D). This expression is close to the oft-quoted limit 2.5D (D in millimetres) for small apertures, but gives a more realistic (lower) maximum magnification for apertures over approx 200 mm. However, note that under certain circumstances higher magnifications may be useable. For example, when trying to split close double stars it is usually not so much the stars themselves that are of interest as their diffraction patterns. Under excellent seeing conditions it is possible to use an eyepiece that will deliver a Ramsden disk of only 0.25 mm or less diameter. Such a high magnification will not necessarily resolve a close double, but if it indicates a diffraction pattern that is slightly elongated this provides a good indication that the star is a double.
The figure to the right shows the curves of maximum and minimum magnification: eyepieces should usually lie in the zone between the two.
As a general guide, the highest magnifications indicated by the upper curve are only occasionally useful when seeing conditions are very steady and the subject is high contrast, e.g. observing double stars. Planetary detail generally requires lower magnification in order to increase contrast in the image. Lower powers are used with dark skies to observe extended objects such as loose star clusters.
Note that the brightness of a point source such as a star is independent of the magnification of the telescope and is determined by the diameter of the OG or mirror. Conversely, for an extended object such as a nebula, higher magnification will result in a dimmer image because the light from the object is spread over a larger image. Because of this, the observer can increase the contrast of an image, to combat light pollution for example, by use of a high magnification to dim the background sky while leaving star images intact.
The following table provides a brief description of the main properties of the more common types of eyepiece.
Type
Pos/
Neg
Appar.
Field
(°)
Eye Relief
(fraction of e/p FL)
Aberrations
Transmiss.
(%)
Notes
Table 1. Properties of common eyepieces.
When buying an eyepiece, consider the application, the magnification and field of view required and balance these against other aspects of the various designs on offer. There is really no such thing as a general purpose eyepiece! It is difficult to give hard and fast recommendations, but the following guidelines are generally helpful:
David Payne, C Peter Davies & Neil Morley