OASI: Dawes limit

The Reverend William Rutter Dawes (19 March 1799 - 15 February 1868) owned many telescopes over the course of his astronomical observing career. Perhaps the most notable is the instrument nowadays known as the "Thorrowgood Refractor" (named after a subsequent owner); it is currently owned by the Royal Astronomical Society and on loan to the Cambridge University Institute of Astronomy. It is a 200 mm aperture refractor of 2.9 m focal length.

Like his contemporary, the Reverend Thomas William Webb (14 December 1807 - 19 May 1885) (who went on to write "Celestial Objects for Common Telescopes"), Dawes was interested in deep sky objects. He compared the performance of his many telescopes and derived the formula that became known as "The Dawes Limit".

The limit describes the finest detail that can be observed through a telescope under ideal seeing conditions. This is also known as "resolving power". Here is the formula:

where R is the resolving power of the instrument in arcseconds and D is the aperture (diameter of the main lens or mirror) in millimetres.

Note that under typical UK skies, a telescope may exhibit an effective resolving power much inferior than its theoretical value calculated as above.

The Tomline Refractor has an aperture of 258 mm, and formula 1 gives its resolving power as 0.4 arcseconds. Thus, under ideal conditions, it will show a double star with separation greater than this value as two stars, but one with smaller separation as a single star.

What does resolving power mean in relation to an extended object (i.e. one that presents a definite angular size and is not just a point source)? Well, consider a right angled triangle with a vertex of angle R at the telescope, the adjacent side of length d being the distance to the object under observation and the opposite side of length L representing the diameter of the smallest feature visible on the object. (The diagram to right shows the situation when observing a lunar crater.) The angle presented by the object is given by

Rearranging formula 2 as L = d tan R provides the diameter (L) of the smallest feature corresponding to the resolving power (R) of a telescope.

The following table shows, for telescopes of various aperture, D, under ideal conditions, the resolving power R and diameter of smallest visible lunar crater, L, with the Moon at mean distance [1]. The table quantifies the familiar notion that, for a body at a given distance, a larger aperture will resolve finer detail. The aperture of the Tomline Refractor is marked * and that of the gargantuan Keck Telescope on Mauna Kea by **.

D (mm)	R (")	L (km)
25	4.6	8.5
50	2.3	4.2
75	1.5	2.8
100	1.2	2.1
125	0.9	1.7
150	0.8	1.4
175	0.7	1.2
200	0.6	1.1
250	0.5	0.8
258*	0.4	0.8
300	0.4	0.7
350	0.3	0.6
400	0.3	0.5
450	0.3	0.5
500	0.2	0.4
10,000**	0.01	0.02

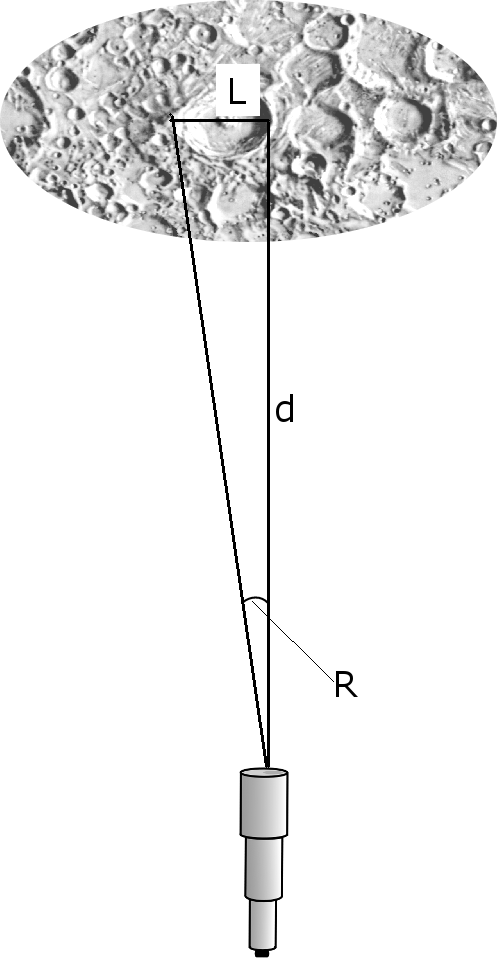
Observing an extended object.

As another example, the smallest feature visible with the Tomline Refractor on Jupiter, assuming that it is at a distance of 5 Astronomical Units, or 750 million km, is of diameter 1635 km. Now, consider the Galilean satellites of Jupiter and their diameters:

The size of the moons, in relation to the resolving power of the Tomline Refractor, explains why we are only able to discern them as slightly extended (non-point) sources, and are unable to resolve any surface detail.

On the other hand, on Jupiter itself, with (equatorial) diameter 143,000 km, we are able to resolve detail down to almost 1% of the size of the planet.

The current minimum size of the Great Red Spot (GRS) is approximately 24,000 km in longitude (east-west) by 12,000 km in latitude (north-south). How small a telescope can see the feature? Formula (2) tells us that the angular diameter in latitude of the GRS is tan^-1 12,000 /750,000,000, or 3.3 arcsec, and formula (1) gives the corresponding value of D as 35 mm. The first telescopes had apertures around this size, and the GRS has been under continuous observation ever since.

Footnote

[1]

The distance, d, from telescope to crater is taken as the mean geocentric distance of the Moon less the radius of the Moon less the radius of the Earth. This is evaluated as: 384,000 - 6378 - 1738 = 376,284 km. Values are taken from the "Explanatory Supplement to the Astronomical Ephemeris", P. Kenneth Seidelmann (Ed.), University Science Books, 1992.