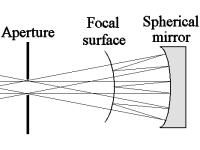
 Fig 1. Overcoming spherical aberration via a small aperture stop in front of a large mirror.
Fig 1. Overcoming spherical aberration via a small aperture stop in front of a large mirror.
Orwell Astronomical Society (Ipswich)
Construction Of A Schmidt Camera
Issues of Sky & Telescope magazine in the mid-1980s carried many photos of Halley's Comet. I noticed in particular one montage in the form of a double page spread of seven shots that all had been taken with Schmidt cameras of various sizes. Not only is this the first return of Halley's Comet to be studied by spacecraft; it is also the first time it has been photographed with these extremely powerful cameras. Invented in 1930 by Bernhard Schmidt, the Schmidt camera has become one of the most useful tools of modern astronomy: it is ideally suited to photographing large, faint objects, for example nebulae and galaxies in addition to comets. Shots of star fields in the Milky Way are also impressive showing maybe 10,000 stars on one negative! This article discusses different types of telescope, explains why the Schmidt camera is so useful and gives a brief overview of construction of a small Schmidt camera.
Short biography of Bernhard Schmidt (1879-1935)
A description of the limitations of conventional telescopes highlights the benefit offered by the Schmidt design. Conventional telescopes come in two basic forms: refractor and reflector. The refractor, in its simplest form, was invented around 1608 in Holland and was developed as an astronomical tool by Galileo Galilei beginning in 1609. Early refractors had a single objective lens to form the image which was magnified by a simple eyepiece. There were two main disadvantages with this design. Firstly, the glass of the lens focused light of different colours to different points along its optical axis, resulting in indistinct, coloured images, an effect known as chromatic aberration. Secondly, spherical aberration meant that rays of light which passed through the edge of the lens came to a different focus to those which passed through its centre. Efforts to overcome spherical aberration went to extreme lengths, literally! By making the focal length very long, spherical aberration can be reduced; in the mid‑1600's, telescopes as long as 30 m were sometimes used. John Dollond remedied this desperate situation in about 1757. He realised that by making the main lens a compound, composed of two individual lenses made from different types of glass, it was possible to largely cancel out both chromatic and spherical aberrations. As a result of this advance, refracting telescopes could be made with much larger lenses but much shorter focal lengths. The state of the art was reached in the late 19th century with the completion of the 1.02 m refractor at Yerkes Observatory near Chicago, still the world's largest refractor. The Yerkes refractor represents the largest such instrument that can be built with current technology: above a diameter of approximately 1 m, in order to retain structural integrity, the objective lens needs to be very thick which, unfortunately, means that it absorbs a lot of light, is extremely heavy and sags under its own weight, distorting the image.
The reflector was invented around 1660 by Isaac Newton. One immediate advantage of the reflector over the refractor is the absence of chromatic aberration; all colours of light are reflected to the same extent. However, if a simple spherical mirror is used, it will introduce spherical aberration. This can be overcome by re-figuring the spherical mirror, changing its shape slightly into a parabola. However, this solution is not ideal because although it eliminates spherical aberration it introduces comatic aberration or coma. A parabolic mirror focuses parallel rays of light hitting the edge and centre at a single point. However, for parallel rays incident at an angle, the parabolic mirror focuses those from the edge and the centre at different points so that an image of a star becomes not a point but a fan or comet shape, a distortion which gives this type of aberration its name. As the angle of the incoming light increases the distortion becomes worse so that the area of sky in sharp focus is very limited.
Schmidt knew of the limitations of conventional telescopes and wanted to design a new type of instrument which would have a very large field of view yet be free of the major aberrations, and have a large diameter compared to focal length, that is, a high photographic speed. His design incorporates elements from both refractors and reflectors but also has completely new features. He realised that a new design would have to have a mirror to eliminate chromatic aberration and that the mirror would have to be spherical to eliminate coma. This was a good start but of course left the problem of spherical aberration. Remembering the trick used by the 17th century astronomers of using a very small aperture, one possibility was to use a small aperture stop some distance in front of the large spherical mirror. Figure 1 illustrates the principle, showing that it allows a large field of view to be obtained on a curved focal surface with low spherical aberration provided the diameter of the stop is less than about 10% of the focal length of the mirror.
The problem with the above approach, of course, is that it supports only a small aperture. Schmidt's stroke of genius was to make the aperture very much larger and to place in it a weak lens or corrector with a special curvature. (Weak in this sense means that the lens has only a slight effect on light passing through it.) The corrector functions as follows. Firstly, because its curvature is very shallow, it affects light of different colours in essentially the same way, and therefore does not introduce chromatic aberration. Secondly, its curvature is figured to cancel out the spherical aberration of the mirror. Thirdly, and importantly, it affects light passing through it at large angles essentially the same as light incident along its optical axis, meaning that the field of view is large. For this reason, the mirror is always larger than the corrector; for example, the Schmidt camera on Mount Palomar has a 1.22 m diameter corrector but a 1.83 m diameter mirror and can photograph an area of the sky with a diameter of 6° (about 12 times the diameter of the Moon).
The diagram below shows the basic design of the Schmidt seen in cross-section. Light enters from the left and passes through the corrector. It can be seen from the shape of the latter that light passing through the edge diverges whereas light passing through the central region converges - exactly cancelling the spherical aberration of the mirror. Because of the symmetry of the system, illustrated in the previous diagram, the focal surface is curved towards the mirror so that the film has to be spring loaded to conform to this curve. Although this sounds rather difficult it becomes a problem only with short focal lengths. The curves on the corrector have been grossly exaggerated in the diagram. By way of a real scenario, in my camera, the corrector has a diameter of 150 mm and a maximum deviation from flat of only 0.004 mm on each side: it looks just like a flat, clear disc of glass!
The first decision is: what size of camera do I want? There are several considerations here, the most important being: size of the finished instrument, photographic speed and field of view. The question of size should be considered seriously: remember that the camera must be mounted equatorially and driven to follow the stars for up to maybe 30 minutes. Photographic speed determines the maximum exposure because if the camera is very fast, say f/1 or f/1.5, background sky fog will severely limit exposure time. Photographic speed also determines to some extent the field of view; between f/2 and f/3 the field will be about 10° to 5° - this is a good range being intermediate between ordinary SLR camera lenses and telescopes. When everything is considered a camera with a 150 mm corrector and a speed of about f/2.5 is a good general purpose instrument, and these are the parameters of the instrument that I determined to build.
The Primary Mirror
As mentioned above, the primary mirror is always larger than the corrector in order to collect light from a wide field. For a 150 mm corrector a 220‑230 mm mirror is ideal and I opted for a mirror of 220 mm diameter. The details of mirror making are too involved to go into here but there are several books, listed below, which describe the methods involved. The conventional method for grinding mirrors is to use two discs of equal size, one of which becomes the mirror and the other the tool. However, for Schmidt primaries, as the curves required are very deep, it is quicker to use a smaller diameter disc as the tool. For my 220 mm mirror I used a 150 mm tool. After grinding, polishing should ideally be carried out with a full sized polisher, however, having used a small tool there is no full sized disc with the required curve on it. I overcame this problem by casting a resin plastic disc in the curve of the mirror (coated with grease to prevent adhesion) and then stuck this to a full sized, flat glass disc. I then made the polishing lap in the usual way (see [1]). Figure 3 illustrates the mirror, silicon rubber mould and and polishing lap.
The Corrector Plate
When the spherical primary mirror is complete and its radius of curvature has been accurately measured the shape of the corrector can be calculated. The equation describing the curve is:
Δ = k(x4-Ar2x2) / ( 4(ε-1)R3 )
where
Δ is the deviation from flat,
x is the radius of the zone under consideration,
r is the clear radius of the corrector,
ε is the refractive index of the glass,
R is the radius of curvature of the mirror,
k is a constant: 0.5 if equal curves on both sides of the glass or 1 if all the correction is one one side,
A is a constant, either 1.0 or 1.5, determining the overall shape.
The problem then becomes one of devising a test to show that the shape is the one required. I devised a test for the corrector based on placing it in contact with an optical flat and measuring the interference fringes produced with monochromatic light. The air gap between corrector and flat is given by the above expression for Δ. By manipulating the equation, it is possible to predict where the bright interference fringes should appear. The positions, x, for bright fringes are given by the formula below. Reference [2] gives full details of the test.
x2 = (Ar2±(A2r4-2(n+½)Kλ)0.5) / 2
where
n is an integer, 0, 1, 2, 3...,
K = 8(ε-1)R3,
k = 0.5 (i.e. equal curves on each side of the corrector),
λ is the wavelength of monochromatic light used in the test.
Armed with the above test I started work on the corrector. I bought a suitable disc of optical glass from H V Skan Ltd [3]. I first ground both sides flat and parallel using two other discs, grinding in pairs in the sequence 1 on 2, 2 on 1, 1 on 3, and so on. (This is the usual method for making an optical flat - see [4], [5] and [6].) I checked the sides to see if they were parallel by measuring the thickness around the edge of the plate with a micrometer; this indicated a constant thickness to within a few microns. I polished the plate to obtain a flat surface on both sides giving straight interference lines.
Only after the above preliminaries did I start work on figuring the corrector. I used a graded polisher based on petal shapes related to the intended figure. The amount of polishing at each zone of the plate was proportional to the required depth of the curve. I used a polishing action, called drag polishing, comprising very short strokes across the centre of the plate. I regularly applied the interference test to indicate how the work was going. Final stages of figuring involved only one or two minutes' work between each test to achieve the required accuracy. Figure 4 shows the interference pattern for my corrector after figuring was complete, illustrating the fringes from centre to edge on an optical flat illuminated by a 632.8 nm helium-neon laser.
As mentioned above the focal surface of a Schmidt camera is curved towards the mirror, the radius of curvature being half that of the mirror. To make the curved surface I used the same technique that I employed to make the full sized tool for a polisher. I ground a glass disc to the correct curvature and used it as a mould to cast a convex resin plastic disc. The plastic resin is available from model shops and is the type used for making, for example, chess pieces from rubber moulds. I smoothed the curved surface by fine grinding on the concave glass template. This gave a plastic focal surface to which discs of cut film can be loaded and held in place with a retaining ring and springs.
At this point in construction of a Schmidt camera, the remainder is straightforward! Problems that do remain before the first photos are taken include:
The references below give many helpful ideas.
I measured the focal length of the completed instrument at 400 mm, giving an f-ratio of f/2.6. Figure 5 shows a negative image of M51 captured with the instrument.
[1]
M J Harlow, A Silicone-rubber Pitch-lap Mould, in Sky & Telescope, vol 66, page 454, 1983.
[2]
M J Harlow, Interference Test for Schmidt Correctors, in Telescope Making #27, page 28, spring 1986.
[3]
H V Skan Ltd, 425-433 Stratford Road, Shirley, Solihull, West Midlands, B90 4AE.
[4]
A G Ingalls (Ed), Amateur Telescope Making (in 3 volumes), published by Scientific American.
[5]
J Texereau, How to Make a Telescope, Willmann-Bell Inc.
[6]
A S DeVany, Master Optical Techniques, John Wiley.
Mike Harlow